Correlation of Computational Modeling to Experimental IR and Raman Data of Structural Units found in Borosulfide and Borate Glass
Kyle Kruse
Abstract
Ab-initio and semi-empirical methods were used to obtain optimized geometries and vibrational frequencies for BO3, BO4, B3O3, B3O6, B5O10, BS3, BS4, B3S6, and B4S9 structural units. These units have been observed in borate and borosulfide glasses using techniques such as TOFMS, NMR, Raman, and FTIR. Theoretical results of calculations using various basis sets and levels of theory were compared to experimental IR and Raman data. Calculations upon similar borate and borosulfide units were compared to examine the effect of replacing oxygen atoms for sulfur atoms. The computed vibrational frequencies agree well with experimental IR values.
Introduction
Computational modeling is a process in which structures and reactions of a molecular input are predicted by computer simulation calculations. Each calculation is performed under different parameters based on the fundamental laws of physics. These parameters are comprised of different theoretical approximation methods and basis sets.
In the Gaussian program, both ab-initio and semi-empirical theoretical methods are applied to make approximations upon the calculations concerning the energy of many-body systems and to minimize unavoidable residual error while keeping the calculations plausible. The ab-initio methods are purely based upon the first principles of quantum mechanical chemistry and include only empirical data. These ab-initio calculations are not exact, but contain a small acknowledged error margin. Unlike the more accurate ab-initio, a semi-empirical calculation makes many approximations from experimental data. The semi-empirical method is more commonly applied to larger molecules decreasing the complexity and the time of the calculation.
The two ab-initio approximation methods used for geometry optimization and vibrational frequency calculations were the Density Functional Theory (DFT) and the Hartree-Fock Theory (HF). Overall, the DFT method provided vibrational modes with calculated frequencies that correlated better with experimental frequencies than the HF method did. What makes the Density Functional Theory different than other approximations is that this method takes into account the electron density, whereas many others are based on a complex many-electron wavefunction[1]. From these calculations, the self-consistent field (SCF) energy and zero point energy were determined. These values are important since the SCF energy is the total energy of the system, and the zero point energy is the lowest possible energy that a quantum mechanical system can have. Zero point energy is also used to extrapolate the calculated quantities to zero Kelvin, refining the determination of the electronic energies.
For each calculation, there is a choice of basis set to apply to the computation. A basis set is a mathematical representation of the molecular orbitals within a molecule. Basis sets are often represented as a number with a hyphen followed by two or three more numbers. The number to the left of the hyphen indicates the number of Gaussian molecular orbitals and the hyphen represents a split valence set. The two or three numbers on the right side of the hyphen account for the basis functions corresponding to each atomic orbital. The more the number of atomic orbitals, the more accurate the calculation is due to fewer limitations on electron movement within a molecular orbital[2].
A computational program can calculate a number of different properties of a molecular unit. The most essential of these calculations is geometry optimization. Geometry optimization is the process of finding equilibrium between molecular structure and resultant energy, based on the observation of the molecular potential energy surface. The potential energy surface represents a link between bond distance and the energy associated with the nuclear positions. A structure is optimized when a global minimum is located, which indicates the lowest energy of repulsion and attraction between the atoms in the structure. The first derivative of the potential energy surface, also known as the gradient, helps the program find the global minimum by giving a description of the slope and indicating the direction in which the energy decreases most rapidly from the initial input. This optimization process is complete when the convergence criteria are met. These criteria consist of making the forces and the root-mean-square of the forces as close to zero as possible and making the calculated displacement of the atoms and its root-mean-square zero. With an optimized geometry, bond energies,
bond lengths, bond angles, and dihedral angles can be determined. For the proper calculation of any other parameters, geometry optimization must be completed to a basis level that is equivalent or higher than the parameter to be calculated[2].
![]()
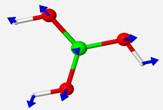 Once
the geometry is optimized, each structural unit undergoes a vibrational
frequency calculation. This is a calculation of the modes of vibration, or
direction and magnitude of nuclei movement in the ground and excited states.
The number of modes of vibration for nonlinear molecules is found by the
equation: 3n−6, where n is the number of atoms. A linear
molecule has 3n−5 normal modes of vibration because the rotation about
its molecular axis does not produce a change in dipole moment, preventing its
observation.
Once
the geometry is optimized, each structural unit undergoes a vibrational
frequency calculation. This is a calculation of the modes of vibration, or
direction and magnitude of nuclei movement in the ground and excited states.
The number of modes of vibration for nonlinear molecules is found by the
equation: 3n−6, where n is the number of atoms. A linear
molecule has 3n−5 normal modes of vibration because the rotation about
its molecular axis does not produce a change in dipole moment, preventing its
observation.
The frequencies of the vibrations are approximated by the quantum harmonic oscillator equation:
E = (n+ �)[hω/2π]
where n= energy level, h=Planck�s constant, and ω is the angular frequency. The energy of each vibration corresponds to a particular frequency at which the structure bends or stretches. These calculated frequencies of the vibrations are either located on the experimental infrared spectra if a change in the permanent dipole occurs or observed on Raman spectra if the polarizability changes during the vibration[2].
The general application of computational chemistry is to predict unobserved chemical and physical phenomena. The present research is centered on using computational chemistry to obtain a better understanding of glass structure, particularly borate and borosulfide glass. Glass structure is ambiguous because at the molecular level, glass consists of a continuous random network, where the building blocks of this network are fused together in an unsystematic pattern of cations and glassformers[3]. The randomness of the glass structure is unique to the components that create its matrix.
Glass is usually composed of a glassformer and a modifier. Glassformers are exactly what their title insinuates- substances that produce �good� glasses. Many substances can produce glass, only a few can produce good glass. Typically, these glassformers are oxides. Examples of such substances are silicon oxide and boron oxide which are common components of everyday glass. The role of a modifier in glass is to alter the physical properties of the glassformer by integrating itself into the glass matrix. Examples of modifiers are cations like Pb2+, Li+, or Na+.
The calculations are performed in an effort to gain insight on the randomness of borate and borosulfide matrices by visualizing the vibrational modes of their structural units under theoretical conditions. It is hoped that from gathered information, one could better understand and formulate predictions on the production and stabilization of the unique networks created by distinct components.
Experimental: Gaussian 2007
Structural units found in borate and borosulfide glasses were reconstructed in an open editor format with hydrogen atoms placed on the terminal oxygen or sulfur atoms to stabilize the molecule. In Gaussian 2007, each unit has its geometry optimized under a 6-311+G(d,p) basis set with the exception of the B3O3H3 unit. The B3O3H3 geometry was optimized under a 6-311+G(d,p) basis set and also, a 3-21G basis set for comparison to a calculation done in previous research[4].
Once the geometry of each unit was successfully optimized, vibrational frequency calculations were performed. Initial calculations for the BO3H3 and B3O6H3 structural units were performed using both the restricted Hartree-Fock (RHF) method and Density Functional Theory (DFT) for comparison of the two approximation methods. The restricted Hartree-Fock approximation method is applied when all electrons are paired and the shells are considered closed, whereas the unrestricted HF method is used when electrons with unpaired spins are present, requiring different molecular orbitals to differentiate between unpaired electrons. Soon after these calculations were completed, the decision was made to only use the DFT approximation method. DFT was chosen over the HF method because calculations performed under the DFT method were displaying results that were closer to experimentally found IR values. The DFT method also is less demanding on the computer program than the HF method which allows for faster calculation time.
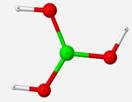
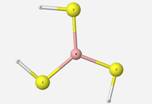
Using only the DFT approximation method, the geometry optimization and vibrational frequencies of the structural units of BO4H4, B5O10H4, BS3H3, BS4H4, B3S6H3, and B4S9H4 were performed. Unfortunately, only a few experimental frequencies were found for the borosulfide units that correlate with the IR active calculated vibrational modes. This was not too troubling considering that the sole purpose of the observation of these borosulfide units was to compare them to the equivalent borates as an internal check or theoretical comparison upon the program itself to see how the substitution of sulfur for oxygen affects the placement of the vibrational modes in the predicted IR spectrum. Comparisons were achieved by looking at the placement of vibrational frequencies for �signature� vibrational modes relative to particular geometries. For the trigonal planar BO3/BS3 geometries, an umbrella motion is identified, in which is the central boron atom asymmetrically stretches in and out of the plane. The tetrahedral geometries of BO4/BS4 have symmetrical stretching of non-hydrogen terminal atoms, and the ring structures of B3O6/B3S6 have a breathing motion that the oxygen or sulfur atoms of the ring stretch symmetrically in and out appearing as if the structure is breathing.
In performing calculations on the BO4H4 and BS4H4 units, it was assumed that the structures have tetrahedral geometries because any other geometry would weaken the strength of the glass matrix. The optimized geometry of BS4H4 was tetrahedral, but when the BO4H4 is isolated in the program, the geometry was optimized as trigonal planar with the fourth oxygen atom being stretched out from the boron at a length twice as long as the other three B-O bonds(Figure 6). Since this geometry appears to be unfavorable for a stable matrix structure, an attempt was made to place the BO4 unit within a larger structure to observe if a surrounding matrix-like structure can stabilize the BO4 in a tetrahedral geometry. The four terminal oxygen atoms of BO4 were extended out by attaching a boron atom to each of them and creating rings off of the central BO4 unit. The geometry was held identical on each side of the molecule to produce a consistent structure. The final double ring structure had a molecular formula of B5O10H4 and the vibrational frequencies of the central BO4 unit were observed and compared to experimental data.
As mentioned previously, geometry optimization and vibrational frequency calculations were performed for a B3O3H3 planar ring under a 6-311+G(d,p) and a more basic 3-21G basis set. A 3-21G basis set was used for geometry optimization and vibrational frequency calculations to reconstruct the procedure done in previous research[4]. In this procedure, a RHF/3-21G basis set was used upon a B3O3H3 unit and the vibrational frequencies were compared to experimental IR data. It was found that the calculated frequencies of a 3-21G basis are approximately 9% larger than experimental IR frequencies, which happens to be a typical error for this particular basis set. This was corrected by multiplying each calculated frequency by a value of 0.9. Once the calculations performed under a 3-21G basis set were completed, a RHF/6-311+G(d,p) basis set was applied to observe how a higher basis set will match up with the same experimental IR frequencies. The error of this basis set is unknown, so no correction was made to the calculated vibrational frequencies.
The next structure observed is a proposed component in sodium borosulfide glasses[5]. Sodium borosulfide glass contains a high 4-coordinated boron to 3-coordinated boron ratio. This structural unit, known as dithioborate, consists of possibly two 3-coordinated and two 4-coordinated boron atoms or four 4-coordinated boron atoms depending if bonds to a central sulfur atom exist.
The final structure of B3O7H4Li was not found in glass but calculations were done to simulate a glass-like situation. The B3O7H4Li geometry calculation was performed with the sole purpose of observing how the program would react to the presence of a cation in the structure, as commonly found in glass with a modifier present.
The data collected from the successful calculations mentioned above include the total self consistent field (SCF) energy, zero-point energy, the mode of vibration, and the wavelength at which each IR and Raman active mode occurred. No attempt to resolve the modes pertaining to hydrogen movement was made because the hydrogen atoms were placed in the structure for stabilization purposes only.
Results
Table 1 displays the energies, vibrational modes, and the theoretical and experimental frequencies associated with the isolated BO3H3 unit determined by the two approximation methods.
![]()
Table 1
|
Theory |
SCF energy (Hartree) |
Zero-point energy (Hartree) |
Calculated Frequency (cm-1) |
Mode |
Experimental (cm-1) |
|
RHF |
-251.3 |
0.0522
|
733 |
Umbrella motion |
650-700 [6] |
|
926 |
Stretching of B-O |
N/A |
|||
|
1486-1542 |
Asymmetric stretch of B |
1200-1400 [7] |
|||
|
DFT |
-1247.6 |
0.0484
|
667 |
Umbrella motion |
650-700 [6] |
|
873 |
Stretching of B-O |
N/A |
|||
|
1391-1454 |
Asymmetric stretch of B |
1200-1400 [7] |
*Table only contains IR active modes
The calculated frequencies of this free trigonal planar structure (Figure 3) agree well with its experimental vibrational modes even though theory did not account for the matrix structure. The frequencies and vibrational modes determined by the RHF and DFT methods display strong agreement to each other although the DFT frequencies relate more closely to experimental IR values and are an average of 7% lower than the RHF values. The higher frequencies calculated by RHF are most likely due to a consistent error introduced by the broad approximations associated with the normalized many-body system of the Hartree-Fock method.
Table 2 displays the energies associated with the calculations, the calculated frequencies, the corresponding vibrational modes, and the experimental frequencies associated with each vibrational mode.
![]()
Table 2
|
Theory |
SCF energy (Hartree) |
Zero-point energy (Hartree) |
Calculated Frequency (cm-1) |
Mode |
Experimental[5] (cm-1) |
|
DFT |
-1221.4 |
0.032 |
415 |
Umbrella motion |
N/A |
|
430 |
B-S symmetrical stretching |
N/A |
|||
|
767-815 |
B stretching, slight shifting |
~750 |
|||
|
1062 |
B stretching- shifting |
~850 |
*Experimental values listed as �N/A� are frequencies involving motions that are not IR or Raman active
Experimentally, stretching was found for the 3-coordinated boron at 750 and
850 cm-1. These values vary slightly from the calculated frequencies, which is most likely due to the fact that the calculation is done upon a loose structure that is not matrix-embedded.
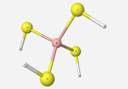 Geometry optimization and
vibrational frequency calculations of BS4H4:
Geometry optimization and
vibrational frequency calculations of BS4H4:
![]()
Table 4 contains the calculated energies and frequencies of IR and Raman active vibrational modes with correlating experimental vibrational frequencies.
Table 4
|
Theory |
SCF energy (Hartree) |
Zero-point energy (Hartree) |
Calculated Frequency (cm-1) |
Mode |
Experimental[5] (cm-1) |
|
DFT |
-1619.8 |
0.042 |
384 |
B-S symmetrical stretching |
N/A |
|
622-653 |
B asymmetrical stretching |
~650, ~750 |
The tetrahedral BS4 contains bond angles of 109� and bond lengths of 1.91 Å.
Experimentally, stretching of the BS4 unit was noticed at 650 and 750cm-1. The calculated vibrational frequency associated with the boron atom asymmetrical stretch was very close in value to the experimentally found vibrational frequency for this mode.
![]()
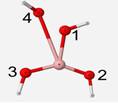
Table 3
|
Theory |
SCF energy (Hartree) |
Zero-point energy (Hartree) |
Calculated Frequency (cm-1) |
Mode |
Experimental (cm-1) |
|
DFT |
-328.0 |
0.0634 |
651 |
Umbrella motion |
N/A |
|
970 |
O-1 and O-4 bending apart |
N/A |
|||
|
1191 |
B stretching in plane |
N/A |
|||
|
1673 |
strong B stretching in plane |
N/A |
The optimized geometry of the BO4 unit is a structure of little symmetry. Bond angles were found to be 142� separating oxygen atoms #2 and 3, 130 � between oxygen atoms #2 and 4, and 86� between oxygen atoms #3 and 4. The oxygen atom #3 is 3� behind the plane and #4 is 20� in front of the plane (Figure 5). B-O bonds for oxygen atoms #1, 2, 3 and 4 are 1.53, 1.32, 1.32, and 2.54 Å, respectively. The bond to oxygen #4 is almost twice as long as the other bonds because the optimized geometry is attempting to expel the fourth oxygen since boron is most stable with only three bonds. Since these geometries are not of the same form, their vibrational frequencies of different vibrational modes cannot be compared.
Table 5 displays the energies associated with the calculations under DFT, the calculated frequencies for the vibrations, the modes of the vibrations, and the experimental frequency associated with each vibrational mode.
![]()
![]()
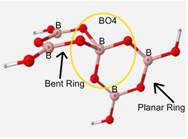
Table 5
|
Theory |
SCF energy (Hartree) |
Zero-point energy (Hartree) |
Calculated Frequency (cm-1) |
Mode |
Experimental (cm-1) |
|
DFT |
-879.8 |
0.11
|
571 |
Stretching of B |
~400[6] |
|
665 |
Breathing of ring 2 with O of BO4 |
~400, ~650[6] |
|||
|
780 |
Stretching of O of BO4 in ring 1 |
~800[6] |
|||
|
1189-1339 |
Stretching of B in BO4 |
~1220[7] |
*Table only contains the vibrational modes associated with the movement of the BO4 unit.
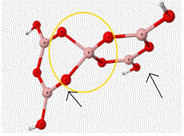
As can be seen in Table 5, this mock glass structure holds the BO4 unit in a tetrahedral geometry and allows for the calculated vibrational frequencies to match up well with the approximated experimental values. Bond angles of the central BO4 unit of this structure are 112� between the oxygen atoms attached to ring 1 and 86� between the oxygen atoms attached to the bent ring or ring 2. B-O bond lengths of BO4 are 1.45Å.
Table 6 shows the calculated frequencies from the previous research[4], the calculated frequencies for this research, the experimental frequencies, and the percent difference of the new calculations relative to the experimental data.
![]()
Table 6
|
Symmetries |
[4]Calculated Frequency |
[4]Calculated x0.9 |
New Calculated Frequency |
New Calculated x0.9 |
[4]Experimental Frequency |
% Difference EQ. 1 |
|
A2�� |
1001 cm-1 |
901cm-1 |
1013cm-1 |
912cm-1 |
910cm-1 |
2.20% |
|
A2�� |
399 |
359 |
434 |
391 |
(380) |
2.90 |
|
E� |
2803 |
2523 |
2901 |
2611 |
2613 |
0.077 |
|
E� |
1532 |
1379 |
1473 |
1326 |
1403 |
5.49 |
|
E� |
1325 |
1193 |
1309 |
1178 |
1200 |
1.83 |
|
E� |
1072 |
965 |
1056 |
950 |
998 |
4.81 |
|
E� |
567 |
510 |
555 |
500 |
530 |
5.66 |
|
A1� |
2823 |
2523 |
2924 |
2631 |
(2616) |
0.57 |
|
A1� |
1060 |
954 |
1074 |
967 |
906 |
6.73 |
|
A1� |
884 |
796 |
851 |
766 |
(800) |
4.25 |
|
E�� |
990 |
891 |
984 |
886 |
1050 |
15.6 |
|
E�� |
231 |
208 |
257 |
231 |
343 |
32.7 |
|
A2� |
1273 |
1146 |
1267 |
1140 |
1477 |
22.8 |
|
A2� |
1224 |
1102 |
1185 |
1067 |
1197 |
10.9 |
*Experimental values in
parentheses are estimated.
*EQ. 1: % Difference = [(Exp. � Cal.)/Exp.] x100%
*Average % difference = 8.32
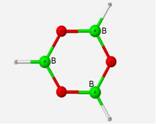
The calculated frequencies of the B3O3H3 structure correlate very well with the computed frequencies of the previous research[4] performed on this structure. In relationship to the experimental values, the calculated frequencies differed by an average 8.32% (EQ. 1). The margin of variation would be lower if not for the few outliers of the E� and A2� symmetries which are only Raman active and were estimated from weak IR combination bands in the IR spectra[7]. The geometry of this ring structure incorporates three trigonal planar BO3 units with bond angles of 120� and bond lengths of 1.36 Å.
Table 7 displays the calculated and experimental values for the B3O3H3 structural unit when performed under a more accurate RHF/6-311+F(d,p) basis set.
Table 7
|
Symmetries |
Calculated Frequency |
[7]Experimental Frequency |
% Difference EQ. 1 |
Symmetries |
Calculated Frequency |
[4]Experimental Frequency |
% Difference EQ. 1 |
|
A2�� |
1014 cm-1 |
910cm-1 |
11.4% |
A1� |
2793 |
(2616) |
6.77 |
|
A2�� |
399 |
(380) |
5.00 |
A1� |
1048 |
906 |
15.7 |
|
E� |
2775 |
2613 |
6.20 |
A1� |
882 |
(800) |
10.3 |
|
E� |
1481 |
1403 |
5.56 |
E�� |
995 |
1050 |
5.24 |
|
E� |
1298 |
1200 |
8.17 |
E�� |
231 |
343 |
32.7 |
|
E� |
1043 |
998 |
4.51 |
A2� |
1256 |
1477 |
14.96 |
|
E� |
572 |
530 |
7.92 |
A2� |
1162 |
1197 |
2.92 |
The calculated frequencies collected under a RHF/6-311+F(d,p) basis set are close in value to the experimental values. The calculated frequencies were approximately 9.8 % different than the experimental values, but unlike with the 3-21G basis set used for the previous calculations of this structural unit, the error of this more accurate basis set is unknown.
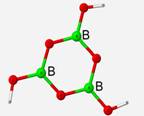
![]()
Table 8
|
Theory |
SCF energy (Hartree) |
Zero-point energy (Hartree) |
Calculated Frequency (cm-1) |
Mode |
Experimental (cm-1) |
|
RHF |
-525.65 |
0.0793 |
485-491 |
Bending of B & O, rocking motion |
400-650 [6] |
|
618 |
Bending of B, ring flex |
400-650 [6] |
|||
|
731-822 |
Bending of B, umbrella motion |
400-650 [6] |
|||
|
876 |
Asym. Stretch of O (breathing motion) |
796 [7] |
|||
|
1313 |
Symmetrical stretching of B |
1200-1400[7] |
|||
|
1469-1582 |
Asymmetrical Stretch of B |
1200-1400 [7] |
|||
|
DFT |
-528.36 |
0.0738
|
454 |
Bending of O, rocking motion |
400-650 [6] |
|
582 |
Bending of O, ring flex |
400-650 [6] |
|||
|
671-740 |
Bending of B, Umbrella motion |
400-650 [6] |
|||
|
804 |
Asym. Stretch of O (breathing motion) |
796 [7] |
|||
|
1220 |
Symmetrical stretching of B |
1200-1400 [7] |
|||
|
1374- 1492 |
Asymmetrical stretching of B |
1200-1400 [7] |
Calculated frequencies displayed an average of 3.78% difference to experimental IR frequencies when the RHF method was applied and 0.71% when the DFT method was used. Extending upon the previous structure, a geometry optimization and vibrational frequency calculation was performed on a B3O6H3 structural unit under both the restricted Hartree-Fock method and the DFT method. This structure is completely planar and symmetrical with bond angles of 120� angles and bond lengths of 1.36 Å.
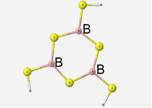 Geometry
optimization and vibrational frequency calculations of B3S6H3:
Geometry
optimization and vibrational frequency calculations of B3S6H3:
![]()
Table 9
|
Theory |
SCF energy (Hartree) |
Zero-point energy (Hartree) |
Calculated Frequency (cm-1) |
Mode |
|
DFT |
-2465.9 |
0.0481 |
297 |
Bending, ring flex |
|
392 - 425 |
Bending of B, umbrella motion |
|||
|
430 |
Asym. Stretch of S (breathing motion) |
|||
|
476 |
Stretching of S in ring |
|||
|
867 |
Asymmetrical stretching of B |
|||
|
921 |
Symmetrical stretching of B |
*No experimental data worthy of comparison was found.
The optimized geometry of this structure contains bond lengths of 1.82 Å, ring B-S-B angles of 110� and S-B-S bond angles of 130�. The terminal S-B-S angles are 115�. The one noteworthy vibrational mode is the asymmetrical stretching of the sulfur atoms. This motion is also described as the breathing motion. Under the DFT method, this motion occurs for this borosulfide unit at 430cm-1.
The geometry optimization and vibrational frequency calculations were performed under the DFT method and collected data are displayed in Table 10.
![]()
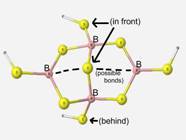
Table 10
|
Theory |
SCF energy (Hartree) |
Zero-point energy (Hartree) |
Calculated Frequency (cm-1) |
Mode |
Experimental Frequency (cm-1) |
|
DFT |
-3685.3
|
0.065
|
314 |
Breathing motion of ring; symmetrical stretching |
N/A |
|
|
|
|
568-597 |
Stretching of 4 coord. B in plane |
~650[5] |
|
|
|
|
647-660 |
Slight stretching of 3 coord. B |
~650[5] |
|
|
|
|
735 |
Stretching of 4 coord. B out of plane |
~750[5] |
|
|
|
|
1012-1045 |
Stretching of 3 coord. B in plane |
~850[5] |
|
|
|
|
1028 |
Stretching of 4 coord. B in plane |
~750[5] |
Accuracy of calculations on this particular structural unit were difficult to determine since the structure is a proposed structure and there is insufficient experimental data for comparison.
![]()
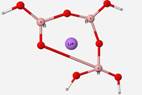
Geometry optimization calculations of B3O7H4Li structural units were also attempted, but were unsuccessful. This unit has not been identified in glass but calculations were done to simulate glass-like situations. The B3O7H4Li geometry calculation was performed to observe how the program would react to the presence of a cation in the structure, as commonly found in glass with a modifier. The geometry contorted itself into unfavorable geometry with the presence of the Li+ ion (Figure 12).
Conclusion & Discussion
Geometry optimization and vibrational frequency calculations were performed on BO3, B3O3, B3O6, and B5O10 structural units found in boron oxide glasses, and BS3, BS4, B3S6, and B4S9 structural units present in borosulfide glasses. With the exception of the B3O3H3 unit, all calculations were performed under a 6-311+G(d,p) basis set and using either Hartree-Fock or Density Functional Theory approximation methods. For calculations concerning the BO3H3 and B3O6H3, both approximation theories were applied and the DFT method proved to provide better correlation of calculated vibrational frequencies to experimentally collected data as seen in Tables 1 and 8 for these structures.
Geometry optimization calculations were completed for the simple borate units of BO3H3 and BO4H4. The calculations were successful for both units but the optimized geometry of the BO4 unit was not as expected. The BS4 geometry takes on a principle tetrahedral geometry and the BO4 resembles a trigonal planar geometry. The 4-coordinated boron structure continuously reverted to a trigonal planar geometry (Figures 5 and 6) with the fourth oxygen atom being stretched out from the central boron since boron prefers to be 3-coordinated. In performing calculations on the BO4H4 unit, it was assumed that the structure has a tetrahedral geometry because any other geometry would weaken the strength of the glass matrix. It is not known for sure why a substitution of sulfur for oxygen results in a tetrahedral structure, but the heavier and larger sulfur atoms are most likely the cause.
In an attempt to hold the BO4 structure in the tetrahedral geometry, the structure of B5O10H4 (Figure 7) was constructed. The double ring structure successfully held the unit within the tetrahedral geometry and the vibrational frequencies of this encased unit matched well with the experimental IR data as shown in Table 5.
The calculated vibrational frequency data collected from the isolated BS3 and BS4 units were compared to borate units of the same geometry. Both structures are perfectly planar with bond angles of 120�. The bond lengths of the BS3H3 structure were 1.82 Angstroms whereas bond lengths found in the BO3H3 structure were 1.37Å. The greater bond lengths of the borosulfide structure are due to the greater repulsion between the larger sulfur atoms and the central boron atom. Since both the BO3 and BS3 have an optimized geometry of trigonal planar, they both have similar vibrational modes. For comparison, signature vibrational modes of particular geometries are observed. For these trigonal planar structures, the umbrella motion vibrational mode occurred about 300 wavenumbers apart at 733cm-1 for BO3 and at 415cm-1 for BS3. The difference in the locations of these modes in the IR spectrum was expected since the heavier sulfur atoms vibrate at a lower energy and lower frequency as compared to the lighter oxygen atoms which vibrate at higher energy and frequency.
The geometry optimization and vibrational frequency calculations of the B3O3H3 structural unit were completed under a RHF/6-311+G(d,p) and a RHF/3-21G basis set. Calculations were performed under a RHF/3-21G basis set to compare calculated frequencies to prior research done under the same parameters. A consistent error was identified in the 3-21G basis set[4], but more investigation is needed to determine the error associated with the RHF/6-311+G(d,p). Overall, the calculated frequencies correlated well with the computed frequencies from the previous research, and both basis sets matched well with the experimental IR frequencies.
Extending upon the previous structure of the B3O3H3, a geometry optimization and vibrational frequency calculation was performed on a B3O6H3 structural unit where terminal oxygen atoms were added to the boron atoms of the ring. This structure is completely planar and symmetrical with bond angles of 120�. Both approximation methods worked well. The calculated vibrational frequencies outside the experimental range varied by an average of 3.78% under the RHF method and the vibrational frequencies calculated under the DFT approximations matched very well with a difference of 0.71%.
The vibrational frequencies of the B3O6H3 were compared to that of B3S6H3. These ring structures contain one signature vibrational mode known as the breathing motion where the oxygen or sulfur atoms of the ring stretch symmetrically in and out of plane. Under the DFT method, this particular mode occurred at 804cm-1 for B3O6H3 and at 430cm-1 for the B3S6H3 unit. The other vibrational modes followed the trend with the vibrational modes of borosulfides appearing at a few hundred wavenumbers less than the borate vibrational modes. Similar to the BO3 and BS3 comparison, the vibrational modes of the borosulfide structures are expected to occur at wavenumbers lower than the vibrational borate modes due to the heavier sulfur atoms.
The final structure observed is a proposed component dithioborate in sodium borosulfide glasses[5]. The calculations upon this structure were performed to determine the stability and feasibility of the structure. The geometry optimization of this unit was a success although there was not sufficient experimental data.
The dithioborate structure had very high calculation time on a regular PC. Since calculations on structures larger than dithioborate would be difficult to obtain with the present resources, dithioborate is observed to represent the best glass matrix-like structure.
Geometry optimization calculations of B3O7H4Li structure was attempted with no success. This structure has not been documented in glass but represents a glass-like situation. Glass typically has a cation present within its structure that often acts as a modifier. In a B3O7H4 ring structure, a lithium ion was added to the center and the optimized geometry output stretched one of the bonds as seen in Figure 12. The unfavorable geometry with the presence of the Li+ ion is possibly due to the introduction of a new mass inside the ring where the ring was not allowed to expand. Further investigation is needed to examine if the program is accepting of the cation or if there are other factors at play.
Overall, the theoretical IR frequencies compared well to the experimental IR data with some slight variances. The slight variances observed between the calculated frequencies and the experimental data are most likely due to the fact that the calculations are done upon loose structures that are not matrix-embedded. It is believed that the calculated values would reflect the experimental values more closely when the units are placed within larger structures simulating a glass matrix. However, from the calculations performed, it was noticed that the program had more difficulty obtaining accurate data for structural units containing bulkier atoms, such as sulfur rather than oxygen. This occurrence is understandable considering that the approximation methods have to take into account another molecular orbital for the sulfur atom. To observe structures containing atoms of large size would most likely not be beneficial since the complexity of the larger molecular inputs leads to larger approximations as a whole.
In the attempt to replicate experimental data through theory, more work is still needed to determine why there are some discrepancies between the different theoretical methods and the experimentally collected data.
This introductory work with theoretical calculations will hopefully open the door for observations for new glass structures. Glass consisting of different components is being produced and examined on a consistent basis by the addition of different modifiers and dopants. It is anticipated that this research can help in the prediction of glass structures with beneficial properties such as stability, strength or thermal properties.
Acknowledgments
Thanks to NSF-REU program for funding research (REU 0649007), Coe College for hosting the research experience and providing guidance in the study, and the chemistry department of McKendree University for all their help.
References
[1] Density Functional Theory. <http://www.physics.ohio-state.edu/~aulbur/dft.html>. (accessed May 2009).
[2]James B. Foresman. AEleen Frisch. Exploring Chemistry with Electronic Structure Methods: A Guide to Using Gaussian. 2nd Ed. Gaussian, Inc.: Pittsburgh, PA. 1996.
[3] Shelby, James E. Introduction to Glass Science and Technology. RSC Paperbacks. Cambridge, UK. 1997.
[4] J.A. Tossell. Paolo Lazzeretti. Calculation of the structure, Vibrational Spectra, and Polarizability of Boroxine, H3B3O3, a Model for Boroxol Rings in Vitreous B2O3. J. Phys. Chem. 1990, 94, 1723-1724.
[5] Martin, Steve. Bloyer, Donald. Cho, Jaephil. Infrared Spectroscopy of Wide Composition Range xNa2S + (1-x)B2S3 Glasses. Journal of the American Ceramic Society. 1993. Vol. 76. pp. 2753-2759.
[6] Pisarski, Wojciech A. Pisarska, Joanna. Ryba-Romanowski, Witold. Structural role of rare earth ions in lead borate glasses evidenced by infrared spectroscopy: BO3↔BO4 conversion. Journal of Molecular Structure. 3 June 2005. Vol. 744-747, p. 515-520.
[7] Ciceo-Lucacel, Raluca. Ardelean, Ioan. FT-IR and Raman study of silver lead borate-based glasses. Journal of Non-Crystalline Solids. 15 June 2007. Vol. 353, p. 2020-2024.
©